Most of the time, when writing code for a Technical Interview or just to brush up on Data Structures & Algorithms skills, sometimes is forgotten two important aspects: Code Quality and being idiomatic in the Programming Language being used.

That’s why I decided to write this post.

**This post will go through some Kotlin concepts.

Understanding the problem

The LeetCode problem states the following,

Given an integer array nums where the elements are sorted in ascending order, convert it to a height-balanced¹ binary search tree.

Before we start off, there are some important observations,

• nums is already sorted.
• An Array is given as an input. So that, accesing to an element will be a constant-time operation $O(1)$.
• The length of nums is at most $10^4$ so the time-complexity must be a good one.
• The resulting Binary Search Tree must be height-balanced.

That’s the LeetCode definition of a Binary Tree,

class TreeNode(var `val`: Int) {
    var left: TreeNode? = null
    var right: TreeNode? = null
}

Algorithm (Recursive solution)

Here’s when Divide and Conquer technique comes into play.

These are the steps to follow to create the BST,

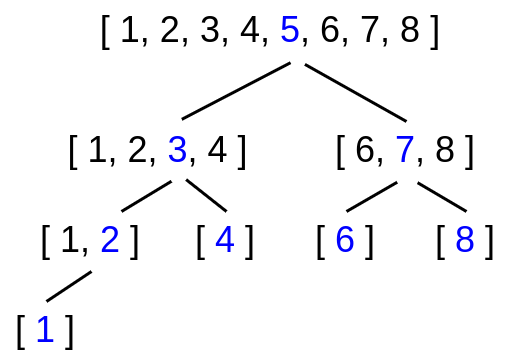
1. Let $n$ the size of the array $A$ and $m = n/2$ the index of the middle element, and pick $A[m]$ as the root of the BST².
2. Consider the two following contiguous subarrays; $A[\ldots m-1]$ and $A[m+1 \ldots]$ respectively with $A$ as a $0$-indexed array, the left and right sub contiguous subarrays.
   • Create the left and right subtrees with $A[\ldots m-1]$ and $A[m+1 \ldots]$ sub contiguous subarrays recursively following the step (1).
   • Repeat recursively until an empty subarray is encountered.

The following diagram depicts the idea,

Kotlin Implementation

class Solution {
    fun sortedArrayToBST(nums: IntArray): TreeNode? {
        fun makeTree(start: Int, end: Int): TreeNode? =
            if (start >= end) {
                null
            } else {
                val mid = start + (end - start) / 2

                TreeNode(nums[mid]).apply {
                    left = makeTree(start, mid)
                    right = makeTree(mid + 1, end)
                }
            }

        return makeTree(0, nums.size)
    }
}

Code Analysis

• Kotlin provides a Null safety in the type system. That’s the reason the type is TreeNode? instead of TreeNode. We can know when a value is nullable or not at compile-time.

• A Local function makeTree was created for building the tree. Note that nums is accessible inside the makeTree function.

• The start and end are used as delimiters in the Binary Search. The reason is to avoid the creation of new subarrays.

• When performing a Binary Search within a range, there’s a common mistake that leads to integer overflow³. That snippet would cause an overflow

  val mid = (start + end) / 2
  

  In order to avoid overflow, the index mid is computed as,

  val mid = start + (end - start) / 2
  

• In Kotlin, if is an expression, it returns a value. Taking advantage of that property, makeTree either returns an empty node (null) or a TreeNode.

  • Returns null if there isn’t a valid range to look up in the Binary Search.
  • A new TreeNode having as element the mid as value and, the left and right subtrees are built recursively.

• The funtion apply is a Scope function. Is used for assigning the values of the left and right subtrees. It’s convenient when modifying the properties of a class in a Kotlin-idiomatic way.

  TreeNode(nums[mid]).apply {
      left = makeTree(start, mid)
      right = makeTree(mid + 1, end)
  } 
  

Complexity Analysis

• Time complexity: $O(n)$, where $n$ stands for the size of the array.
• Space complexity: $O(h)$, where $h$ stands for the height of the BST. The maximum depth of the recursion in the stack is $h$.

Ergo, the BST is built in linear time and the space needed is $h$.